Morse-Potential

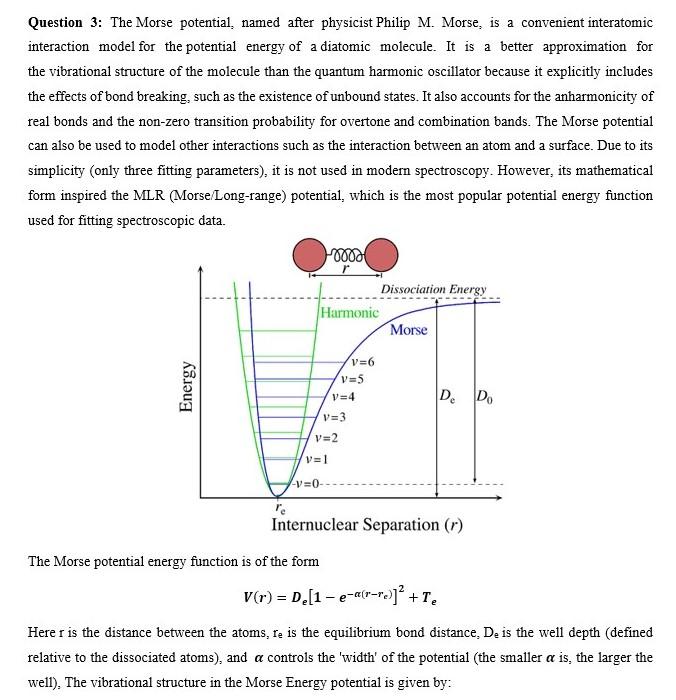
Das Morse-Potential ${\displaystyle V}$ ist ein Begriff aus der Molekülphysik. Der 1929 vom US-amerikanischen Physiker Philip McCord Morse vorgeschlagene Zusammenhang beschreibt den Verlauf des elektronischen Potentials eines zweiatomigen Moleküls in Abhängigkeit vom Kern­bindungsabstand ${\displaystyle R}$ durch eine exponentielle Näherung:

${\displaystyle V(R)=D_{\text{e}}\cdot \left(1-e^{-a\cdot (R-R_{\text{e}})}\right)^{2}}$

mit

• ${\displaystyle D_{\text{e}}}$ die (spektroskopische) Dissoziationsenergie
• ${\displaystyle R_{\text{e}}}$ der Kernabstand mit der geringsten potentiellen Energie und
• ${\displaystyle a}$ eine Konstante (manchmal als „Steifigkeit des Potentials“ bezeichnet)

Diese Größen sind für das betrachtete Molekül charakteristisch.

Da man üblicherweise das Potential im Unendlichen als null definiert:

${\displaystyle V(\infty )=0}$

wird das Morse-Potential häufig in der alternativen Form angegeben:

${\displaystyle V(R)-D_{\text{e}}=D_{\text{e}}\cdot \left(e^{-2a\cdot (R-R_{\text{e}})}-2e^{-a\cdot (R-R_{\text{e}})}\right)}$

Dadurch verschiebt sich das Nullpunktpotential um ${\displaystyle -D_{\text{e}}}$. Diese Verschiebung ermöglicht die Definition eines cutoff-Radiuses, ab dem das Potential nicht mehr berücksichtigt wird.

Die Schrödinger-Gleichung ist mit dem Morsepotential analytisch lösbar. So können die Schwingungsenergien ${\displaystyle E_{\nu }}$ berechnet werden:

${\displaystyle E_{\nu }=h\omega _{0}\cdot \left(\nu {\frac {1}{2}}\right)-{\frac {h^{2}\omega _{0}^{2}}{4D_{\text{e}}}}\cdot \left(\nu {\frac {1}{2}}\right)^{2}}$

mit

• dem planckschen Wirkungsquantum ${\displaystyle \ h}$
• der Schwingungsquantenzahl ${\displaystyle \nu }$
• der Frequenz ${\displaystyle \omega _{0}}$, die über die Teilchenmasse ${\displaystyle m}$ mit der Konstante ${\displaystyle a}$ des Morse-Potentials verknüpft ist

${\displaystyle \omega _{0}={\frac {a}{2\pi }}{\sqrt {\frac {2D_{\text{e}}}{m}}}}$

Heutzutage wird für die Berechnung von Schwingungsenergien eher das RKR-Potential (RKR steht hierbei für Ragnar Rydberg, Oskar Klein und Lloyd Rees) oder das Lennard-Jones-Potential angewendet.

Literatur

• Wolfgang Demtröder: Molekülphysik: Theoretische Grundlagen und experimentelle Methoden. Oldenbourg Wissenschaftsverlag, 2003, ISBN 978-3-486-24974-3, S. 93–94. 
• Ludwig Bergmann, Clemens Schaefer, Wilhelm Raith, Mit Beitragen Von H. Kleinpoppen, M. Fink, N. Risch: Bestandteile der Materie: Atome, Moleküle, Atomkerne, Elementarteilchen. Walter de Gruyter, 2003, ISBN 978-3-11-016800-6, S. 460–462. 
• Gerd Otter, Raimund Honecker: Atome – Moleküle – Kerne: Molekül- und Kernphysik. Vieweg Teubner, 1996, ISBN 978-3-519-03220-5, S. 152–154. 

Einzelnachweise